Statistics & Optimization for Trustworthy AI

Our Research

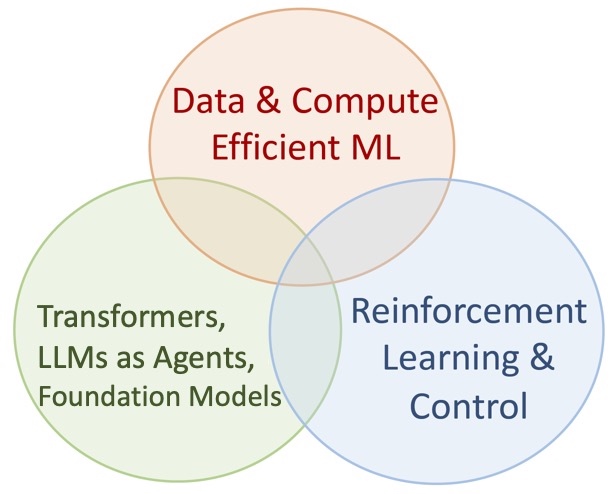
We develop principled and empirically-impactful AI/ML methods

• mathematical foundations of transformers and attention
• trustworthy and efficient language models, LLM systems
• reinforcement learning, control, LLMs as interactive agents
• core optimization and statistical learning theory

News

• I will serve as a Senior Area Chair for NeurIPS 2024.
• New course: Foundations of Large Language Models.
  • Link to syllabus (including Piazza and logistics)
• New paper: From Self-Attention to Markov Models, M.E. Ildiz, Y. Huang, Y. Li, A.S. Rawat, S.O.
• Two papers are accepted to AISTATS 2024 (papers upcoming)
  • “Mechanics of Next Token Prediction with Self-Attention”, Y. Li, Y. Huang, M.E. Ildiz, A.S. Rawat, S.O.
  • “Risk and Emergence of Individual Tasks in Multitask Representations”, M.E. Ildiz, Z. Zhao, S.O.
• Two papers are accepted to AAAI 2024 and one paper is accepted to WACV 2024
  • Class-attribute Priors: Adapting Optimization to Heterogeneity and Fairness Objective
  • Effective Restoration of Source Knowledge in Continual Test Time Adaptation
• Invited talks at USC, INFORMS, Yale, Google NYC, and Harvard on our works on transformer theory
• Transformers as SVMs and FedYolo will appear in NeurIPS workshops
• Two papers are accepted to NeurIPS 2023
  • Max-Margin Token Selection in Attention Mechanism, spotlight paper!
  • Dissecting Chain-of-Thought: A Study on Compositional In-Context Learning of MLPs
• Grateful for the Adobe Data Science Research award!
• Our new works develop the optimization foundations of Transformers via SVM connection
  • Transformers as Support Vector Machines => Twitter thread
  • Max-Margin Token Selection in Attention Mechanism, NeurIPS’23
• Two papers appeared at ICML 2023
  • Transformers as Algorithms: Generalization and Stability in In-context Learning
  • On the Role of Attention in Prompt-tuning
• Two papers appeared at AAAI 2023: Provable Pathways and Long Horizon Bandits
• Papers to appear at AutoML 2023 and ICASSP 2023.
• One paper is accepted to L4DC 2023 as oral presentation.